Variable FlexOlmo

Variable FlexOlmo

I’ve been working on variable-sized experts in MoEs (previous post) using a modified version of Megablocks. The TL;DR from that work: at my scale, I didn’t find efficiencies beyond what you’d get from simply using narrower experts across the board. But since I have this hammer, I’ve been looking for nails.

I’d had my eye on doing a project with Ai2’s FlexOlmo for a while, and it seemed like a perfect nail. The core idea of FlexOlmo is to train specialized experts separately on their own domains, then combine them into an MoE¹. They got good results, and the architecture opens the door to data collaboration. Organizations can train experts on private data without surrendering it, then combine those experts into a more performant MoE model without leaking sensitive information. But training a 4.3B expert isn’t cheap, and in data constrained situations, it doesn’t necessarily make sense to train a model that large. If smaller experts work, that would lower the barrier to participation significantly.

Since I have limited resources, I figured the best way to do this was to prune the expert MLPs of one of the existing expert + public model models that Ai2 released, and use distillation to retrain the model, like these two NVIDIA papers (Muralidharan et al., Sreenivas et al.), as opposed to training new experts from scratch.

So, I took Ai2’s released math expert, pruned its MLPs to various widths, and retrained with knowledge distillation to see how small the expert could get while still contributing to the combined model.

In ~228M tokens of retraining with KLD distillation, I’m happy with the results, and it is a solid proof of concept. Even pruning the expert down to ~800M parameters total improves the Math2 score from 8.1 to 29.1.

Pruning the Math Expert: Shrinking the Expert MLP Layers

I pruned the Flex-math-2x7B-1T math expert to three widths: 8192, 5504, and 2048 (down from 11008). Since the hidden size of the base model has to stay the same, and I didn’t want to touch the attention heads or number of layers, I shrank the expert MLP layers. One thing I’d like to try eventually: pruning different experts by different amounts within the same MoE, with sizing informed by per-expert importance scores rather than arbitrary uniform targets. Variable expert sizes make this straightforward.

Importance Analysis

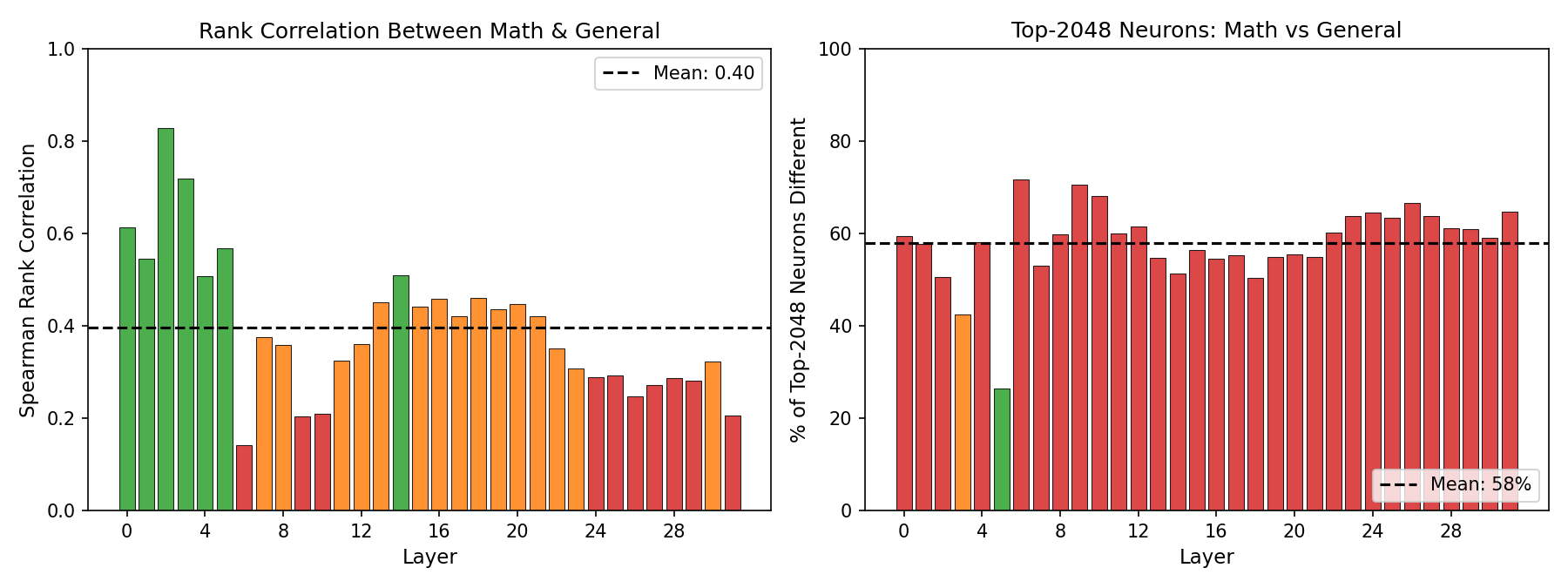
For the 2048 width model, I wanted to test how much the dataset used for importance analysis (the step where we decide which neurons to prune) matters. Not necessarily shocking, but it turns out quite a lot! I tried two datasets: a subset of the math data from dolmino-mix-1124², and general data from the same dataset, which does include some math.

58% of the top-2048 most important neurons are different between the two analyses. The early layers mostly agree on what’s important, but from layer 6 onward the rankings diverge.

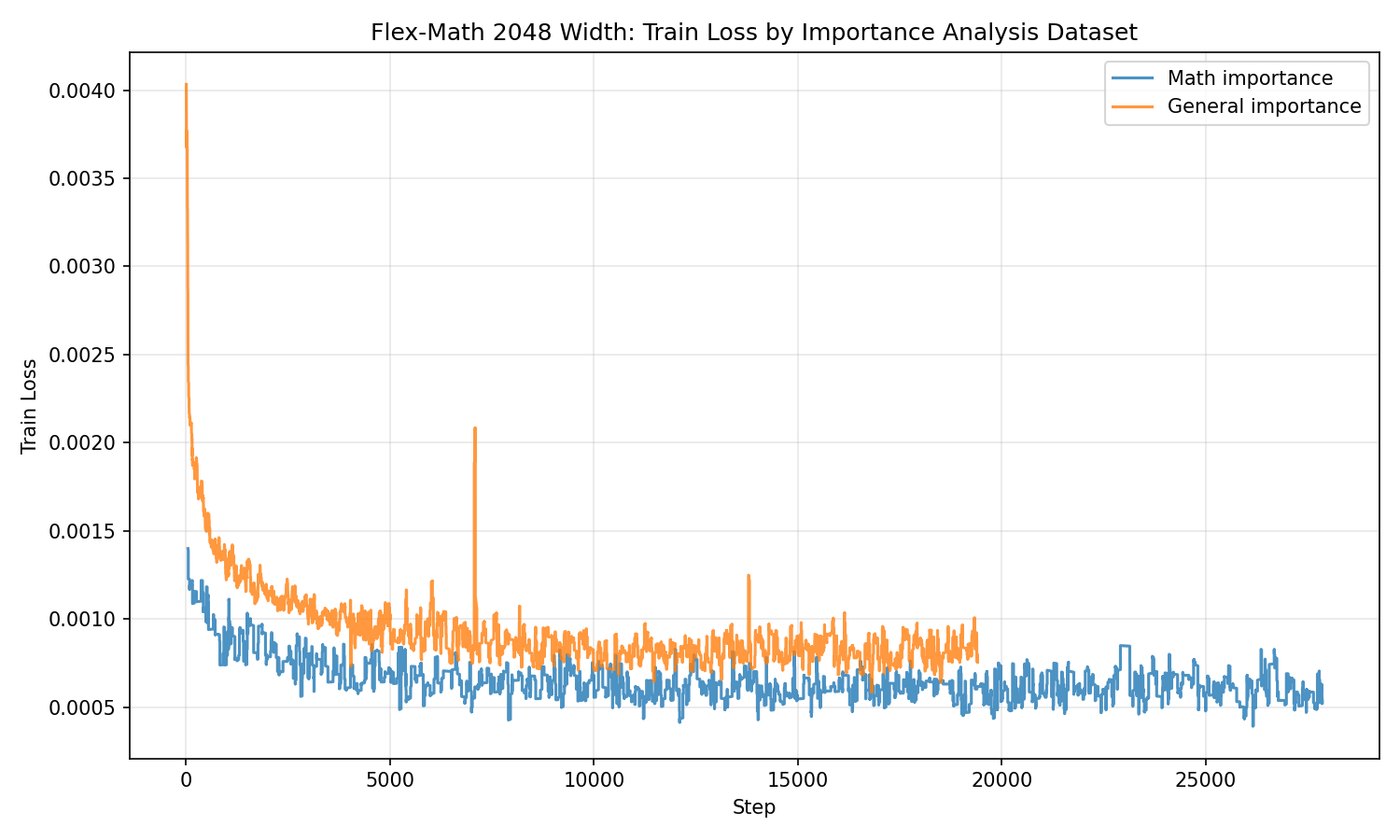
The model calibrated with math data also trained more effectively, achieving consistently lower training loss throughout. Validation loss followed the same pattern. Note that I did stop the general training run early, but it wasn’t going to catch up, and I wanted to move on to training the larger models.

Here are the loss curves of the math and general models, which show that the model calibrated with the math dataset is the clear winner.

Distillation

To be explicit: the teacher is the full-sized Flex-math-2x7B-1T; the student is the pruned model. These models were retrained using distillation with the top 128 logprobs generated by Flex-math-2x7B-1T using the GSM8k, Metamath-owmfilter, and TuluMath subsets of the DOLMino mix dataset (the same dataset that FlexOlmo was trained with), about 620K total documents. Logprobs dataset here.

Performance vs Baseline

Evals

Using LM eval harness (which handles base models well), we got pretty close to the paper’s baseline numbers. Math2 is the macro average of GSM8K and MATH³.

Model	Total Params	Expert Params	Expert Width	GSM8K	MATH	Math2
Public model, no expert4	7.3B	0	—	—	—	8.1
Flex-math-2x7B-1T (baseline)	11.6B	4.3B	11008 (100%)	69.7	35.4	52.5
flex-math-8192	10.5B	3.2B	8192 (74%)	70.1	31.3	50.7
flex-math-5504	9.5B	2.2B	5504 (50%)	66.6	26.8	46.7
flex-math-2048	8.1B	0.8B	2048 (19%)	44.3	13.9	29.1
flex-math-2048 (pruned only, no distillation)	8.1B	0.8B	2048 (19%)	13.1	3.3	8.2

The 8192 model is juust about on par with the full-sized expert. Even the 2048 model (0.8B expert params) scores 3.6x the no-expert baseline. The half-sized expert (5504) is pretty competitive with its larger siblings.

It’s also worth noting how much distillation matters: the pruned-only 2048 model (no retraining at all) scores just 13.1% on GSM8K and 3.3% on MATH, barely above the no-expert baseline. Distillation recovers it from near-broken to 44.3% / 13.9%, a massive improvement for only ~228M tokens of training.

Takeaways

I think this is a pretty good nail!

• I’m particularly impressed with the 2048-width model. Adding just 800M parameters makes the model almost four times as good as the baseline model! I think that seems like very good bang for your buck, especially for training on so few tokens.
• Prune + distill is a good path to making smaller FlexOlmo models
• Choosing the importance analysis dataset wisely can make a pretty substantial difference in the overall performance of the model.
• Smaller experts could make the data collaboration vision of FlexOlmo more viable

Tentative Recipe for Training New FlexOlmo Experts (Untested… for now)

Based on what worked here, I think the recipe for training new FlexOlmo experts would look something like:

1. Do importance analysis on the Flex-public-7B-1T model with the target dataset
2. Prune the MLPs to the desired width
3. Attach those to an untouched public model (as described in the FlexOlmo paper)
4. Train only the expert’s MLP, either with regular old cross entropy loss on the dataset or, even better, using KLD distillation from a strong teacher model.

Limitations

I only evaluated on math benchmarks (GSM8K and MATH). It’s possible that pruning the expert hurts general reasoning or other capabilities that I didn’t measure. Running BBH was going to take like 60 hours on my home system, so I figured I’d just punt and do these. Since we’re pruning a math expert and testing math performance, I think the evals here are the right ones, but broader evaluation would be nice. I also really want to know how FlexOlmo works with post-training. Can we mix a post-trained public model and an expert model with just continued pretraining? Or just post-train the expert model?

1. This glosses over a few details, but I think it’s an ok way to think about it. ↩

2. Using the following files from the dataset: data/math/gsm8k/**/*.jsonl, data/math/metamath-owmfilter/**/*.jsonl, data/math/tulu_math/**/*.jsonl. About a week later, I honestly don’t remember why I only chose those from the dataset. I remember trying to avoid code– MathCoder and a couple other parts of the math dataset are code-heavy, but I don’t remember why I avoided e.g., DolminoSynthMath. Bit of an oversight, but I think we still have meaningful results with a smaller dataset. ↩

3. I think it’s the macro average! I can’t find the exact definition anywhere, but the metrics I found line up with the paper well. ↩

4. Scores reported from the FlexOlmo paper, Table 1. This is the public-only model with no math expert attached. ↩